Notes on Graph Theory (Updating...)
1 Basic counting: sets and tuples
This section lacks a formal definition of the cardinality of a set, offering instead an intuitive explanation of the concept (which refers to the number of elements within a given set). For certain audiences, this approach may be considered insufficiently rigourous. Nevertheless, this is enough for our purpose.
If $X$ is a set, then $|X|$ is the size or cardinality of $X$. Most of the sets we will encounter in this note will be finite (with the frequent exception of the natural numbers $\mathbb{N}=\{1,2,3, \ldots\}$ ).
Our canonical set of size $n$ (where $n \in \mathbb{N}$ ) is denoted by $[n]:=\{1,2, \ldots, n\}.$
The empty set is denoted $\emptyset$.
If $A$ and $B$ are sets, then $A$ is a subset of $B$ if every element of $A$ is also an element of $B$. We denote this by $A \subseteq B$.
If $A$ and $B$ are sets, then their union is $A \cup B=\{x \mid x \in A \text{ or } x \in B\}$ and their intersection is $A \cap B=\{x \mid x \in A \text{ and } x \in B\}$.
The set difference of $A$ and $B$ is $A \backslash B=\{x \mid x \in A \text{ and } x \notin B\}$. The symmetric difference of $A$ and $B$ is $A \Delta B=(A \backslash B) \cup(B \backslash A)=(A \cup B) \backslash(A \cap B).$
If $A$ and $B$ are sets, then their cartesian product is $A \times B=\{(a, b) \mid a \in A \text{ and } b \in B\}$.
If $A$ and $B$ are sets such that $A \cap B=\emptyset$, then we say $A$ and $B$ are disjoint. If we have a union of two disjoint sets, we emphasize this by writing $A \dot{\cup} B$. If $A_1, A_2, \ldots, A_n$ are sets, then we say they are pairwise disjoint if $A_i \cap A_j=\emptyset$ for all $1 \leq i<j \leq n$.
Let $A$ and $B$ be finite sets. Then
- $|A \setminus B|=|A|-|A \cap B|;$
- $|A \cup B|=|A|+|B|-|A \cap B|;$
- $|A \times B|=|A| \cdot|B|;$
- If $A_1, A_2, \ldots, A_n$ are pairwise disjoint sets, then $\left|\bigcup_{i=1}^n A_i\right|=\sum_{i=1}^n\left|A_i\right|;$
- If $A_1, A_2, \ldots, A_n$ are sets, then $\left|\bigcup_{i=1}^n A_i\right| \leq \sum_{i=1}^n\left|A_i\right|.$
Proof. Omitted. ◻
The so-called sum rule holds for disjoint sets: if $A$ and $B$ are disjoint sets, then $|A \cup B|=|A|+|B|$. This follows from Lemma 1.1 (2).
For any integer $k \geq 1$, we define $k$ factorial to be $k !=k(k-1) \cdots 2 \cdot 1$. We define $0 !=1$. For integers $n \geq k \geq 1$, we define the $k$-th falling factorial of $n$ by $(n)_k=$ $n(n-1) \cdots(n-k+1)$. So $(k)_k=k !$.
Let $X$ be a set. A $k$-tuple of elements from $X$ is $\left(x_1, x_2, \ldots, x_k\right)$ where $x_i \in X$ for $1 \leq i \leq k$. Note that the elements of a $k$-tuple need not be distinct. We will denote the set of $k$-tuples from $X$ by $X^k$.
Let $X$ be a set. A $k$-tuple of distinct elements from $X$ is $\left(x_1, x_2, \ldots, x_k\right)$ where $x_i \in X$ for $1 \leq i \leq k$ and $x_i \neq x_j$ for $i \neq j$. We will denote the set of $k$-tuples of distinct elements from $X$ by $(X)_k$.
If $X$ is a set of size $n$ and $0 \leq k \leq n$, then the family of $k$-sets from $X$ is \({X \choose k} =\{A \subseteq X: | A| =k\} .\)
Let $0 \leq k \leq n$ be integers. Recalling that $0!=1$ and we define the binomial coefficient by \({n \choose k}=\frac{n !}{k !(n-k) !}=\frac{(n)_k}{k !} .\)
If $X$ is a set, then the power set of $X$ is the family of all subsets of $X$ : \(\mathscr{P}(X)=\{A \mid A \subseteq X\} .\)
Often we work with subsets of a given "universal set" $X$. In this case we can define the complement of a set $A \subseteq X$ by $A^c=X \backslash A$.
Let $1 \leq k \leq n$ be integers and $X$ be a set of size $n$. Then
There are $n^k$ different $k$-tuples of elements from $X$, so $\left|X^k\right|=n^k$;
There are $n(n-1) \cdots(n-k+1)$ different $k$-tuples of distinct elements from $X$, so $\left|(X)_k\right|=(n)_k$;
There are $n!$ distinct permutations of the elements of $X$;
There are ${n \choose k}$ distinct $k$-sets from $X$, so $\left|{X \choose k}\right|={n \choose k}$;
${n \choose k}={n \choose n- k}$;
${n+1 \choose k}={n \choose k}+{n \choose k-1}$;
$|\mathscr{P}(X)|=2^n$.
Proof. Omitted. ◻
2 Graphs
2.1 Basic definitions
A graph is a pair $(V, E)$ of sets with $E \subseteq {V \choose 2}$. An element of $V$ is a vertex and an element of $E$ is an edge. We denote the set of vertices and the set of edges of a graph $G$ by $V(G)$ and $E(G)$ respectively. The order of a graph $G$ is the number of vertices $|V(G)|$. The size of a graph is the number of edges $|E(G)|$.
If $G$ is a graph and $v \in V(G)$, then the neighbourhood (or $n b h d$) of $v$ is the set \(\Gamma(v)=\{u \in V(G) \mid u v \in E(G)\} .\) The degree of a vertex $v \in V$ is the size of its neighbourhood: $d(v)=|\Gamma(v)|$.
Beware of other different definitions of graphs! All the graphs in this note will be simple, loopless, and undirected. To be precise, a graph is simple if it cannot have multiple edges between two vertices; a graph is loopless if every edge contains exactly two different vertices; a graph is undirected if its edges are 2-sets such as ${u, v}$ rather than ordered pairs such as $(u, v)$ or $(v, u)$. Note that our definition of a graph as $G=(V, E)$ with $E \subseteq {V \choose 2}$ implies immediately that they are simple, loopless and undirected.
Figure 1. A directed graph
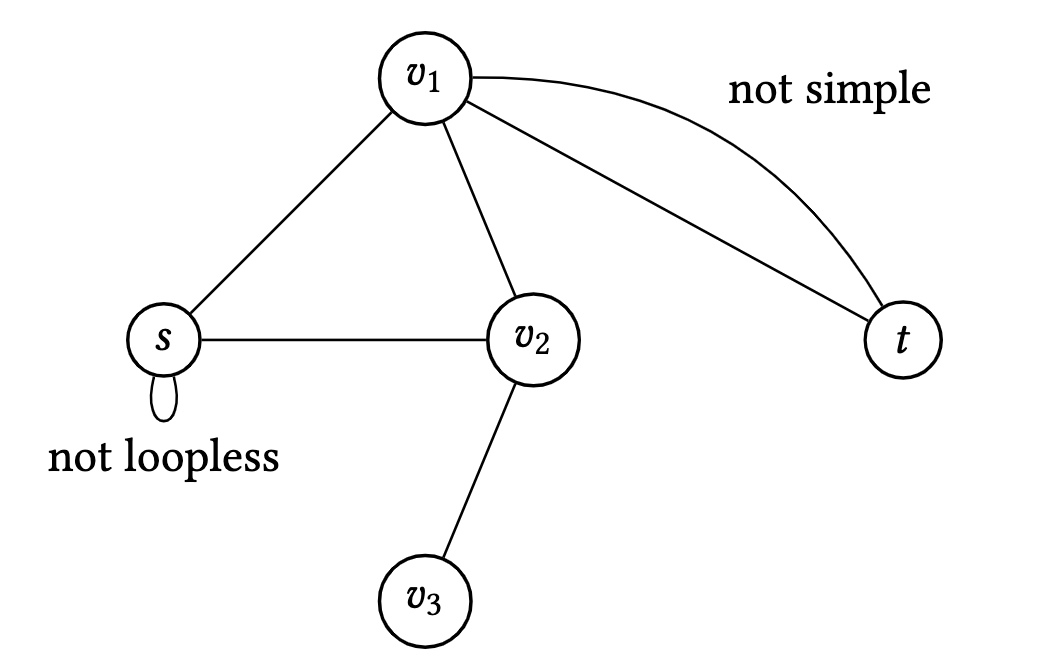Figure 2. An undirected graph which is not loopless and not simple
If $e=\{u, v\}$ is an edge in a graph $G$, with a slight abuse of notation, we will often write this as $e=u v$. Note that this does not imply that the edge has a direction as our graphs are undirected.
If $e=u v$ is an edge, then $e$ is incident to $u$ and $v$.
A graph $G$ is $r$-regular if $d(v)=r$ for all $v \in V(G)$.
The degree sequence of a graph $G = (V, E)$ is the tuple $\left(d\left(v_1\right), d\left(v_2\right), \ldots, d\left(v_n\right)\right),$ where $V=\left\{v_1, \ldots, v_n\right\}$ and $d\left(v_1\right) \leq d\left(v_2\right) \leq \cdots \leq d\left(v_n\right)$.
For any graph $G=(V, E)$, one has \(\sum_{v \in V} d(v)=2|E|.\)
Proof. Omitted. ◻
In any graph, the number of vertices of odd degree is even.
Proof. Omitted. ◻
2.2 Examples of graphs
Recall that for $n \in \mathbb{N}$, we define $[n]=\{1,2, \ldots, n\}$.
$K_n$ is the complete graph of order $n \geq 1$ where
\[V\left(K_n\right)=[n], \quad E\left(K_n\right)= {[n] \choose 2}.\]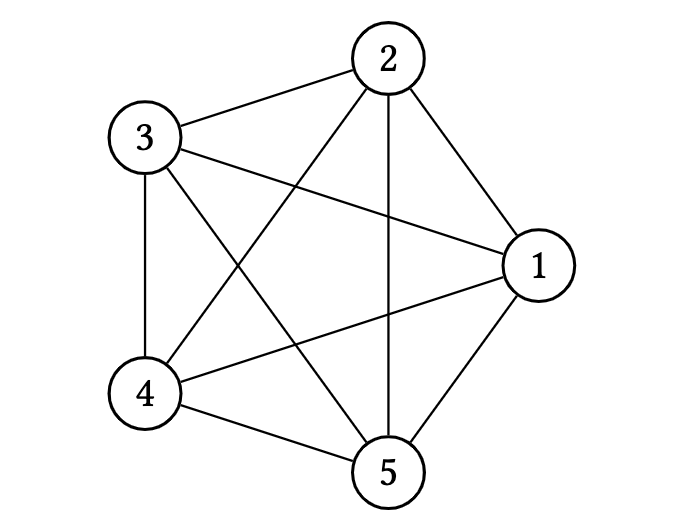
Figure 3. The complete graph of order $5$, $K_5$
$E_n$ is the empty graph of order $n \geq 1$ where
\[V\left(E_n \right)=[n], \quad E\left(E_n \right)=\emptyset.\]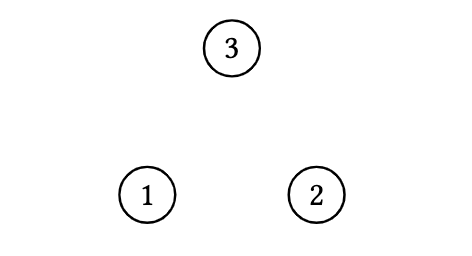
Figure 4. The empty graph of order 3, $E_3$
$C_n$ is the cycle of length $n \geq 3$ where
\[V\left(C_n\right)=[n], \quad E\left(C_n\right)=\{\{i, i+1\} \mid i=1,2, \ldots, n-1\} \cup\{\{1, n\}\}.\]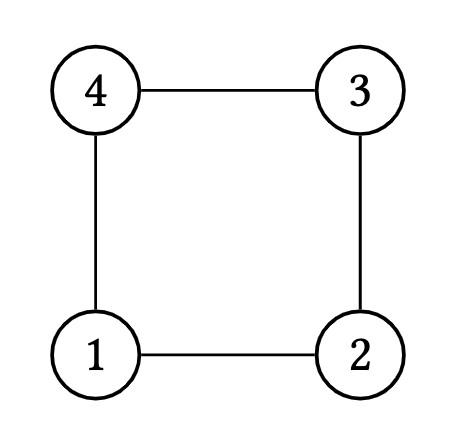
Figure 5. The cycle of order 4, $C_4$
$P_n$ is the path of length $n \geq 1$ (with $n$ edges and $n+1$ vertices) where
\[V\left(P_n\right)=\{0,1,2, \ldots, n\}, \quad E\left(P_n\right)=\{\{i-1, i\} \mid i \in[n]\}.\]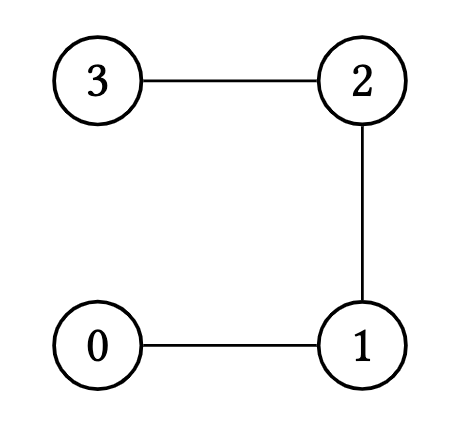
Figure 6. The path of length 4, $P_4$
$K_{a, b}$ is the complete bipartite graph with classes of size $a$ and $b$ $(a, b \geq 1)$ where
\[\begin{aligned} V\left(K_{a, b}\right)&=\{1,2, \ldots, a\} \dot{\cup}\{a+1, a+2, \ldots, a+b\}, \\ E\left(K_{a, b}\right)&=\{\{i, j\} \mid 1 \leq i \leq a, a+1 \leq j \leq a+b\} . \end{aligned}\]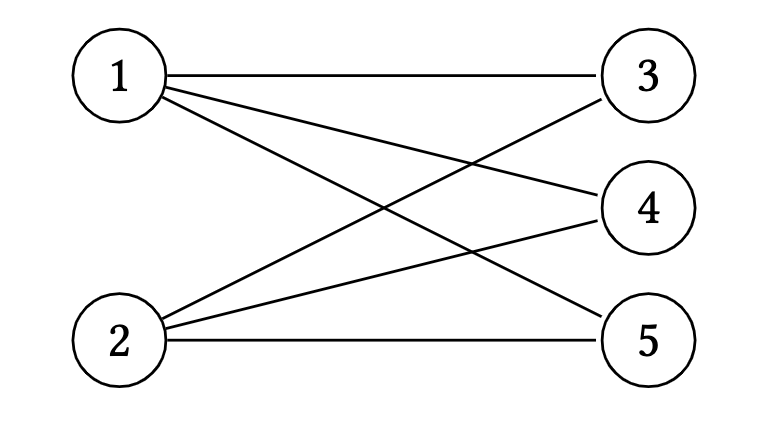
Figure 7. The complete bipartite graph with classes of size 2 and 3
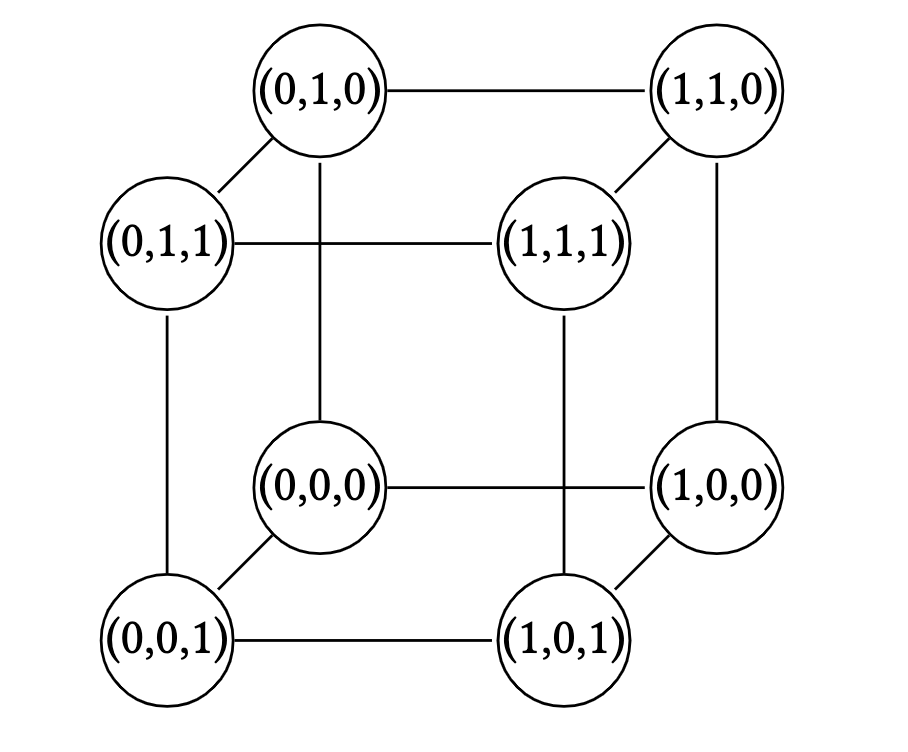
$Q_n$ is the discrete hypercube of dimension $n \geq 1$ where
\[V\left(Q_n\right)=\{0,1\}^n, \quad E\left(Q_n\right)=\{x y \mid x \text{ and } y \text{ differ in exactly one coordinate} \}.\]
Figure 8. The discrete hypercube of dimension 3, $Q_3$